En esta página aprenderás qué es y cómo calcular la inversa de una matriz por el método de los determinantes (o de la matriz adjunta) y por el método de Gauss. Además verás todas las propiedades de la matriz inversa, y también encontrarás ejemplos y ejercicios resueltos paso a paso de cada método para que los entiendas a la perfección. Finalmente, explicamos una fórmula para invertir una matriz 2×2 rápidamente e incluso la mayor utilidad de esta operación matricial: resolver un sistema de ecuaciones lineales.
¿Qué es la inversa de una matriz?
Sea una matriz cuadrada. La matriz inversa de
se escribe
, y es aquella matriz que cumple:
Donde es la matriz Identidad.
¿Cuándo se puede invertir una matriz y cuándo no?
La manera más fácil de determinar la invertibilidad de una matriz es mediante su determinante:
- Si el determinante de la matriz en cuestión es diferente de 0, significa que la matriz es invertible. En este caso decimos que se trata de una matriz regular. Además, esto implica que la matriz es de rango máximo.
- En cambio, si el determinante de la matriz es igual a 0, no se puede invertir la matriz. Y, en tal caso, se dice que es una matriz singular o degenerada.
Principalmente, existen dos métodos para invertir cualquier matriz: el método de los determinantes o de la matriz adjunta y el método de Gauss. A continuación tienes la explicación del primero, pero también puedes consultar cómo invertir una matriz con el método de Gauss más abajo.
Invertir una matriz por el método de los determinantes (o por la matriz adjunta)
Para calcular la inversa de una matriz, , hay que aplicar la siguiente fórmula:
Donde:
es el determinante de la matriz
es la matriz adjunta de
- El exponente
indica la transposición de la matriz, es decir, se tiene que transponer la matriz adjunta.
Comentario: En algunos libros utilizan una fórmula de la matriz inversa un poco diferente: primero trasponen la matriz A y luego calculan su matriz adjunta, en vez de calcular antes la matriz adjunta y después trasponerla. En realidad, da igual el orden porque el resultado es exactamente el mismo. Te dejamos aquí con la fórmula para invertir una matriz cambiada por si prefieres utilizar esta:

A continuación vamos a ver cómo hallar la inversa de una matriz resolviendo un ejercicio como ejemplo:
Ejemplo de cómo calcular la matriz inversa por el método de los determinantes (o de la matriz adjunta):
- Calcula la inversa de la siguiente matriz:
Para determinar la inversa de la matriz, tenemos que aplicar la siguiente fórmula:
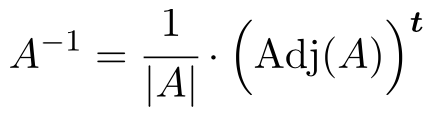
Pero si el determinante de la matriz es nulo significa que la matriz no es invertible. Por tanto, lo primero que debemos hacer es calcular el determinante de la matriz y comprobar que es diferente de 0:
El determinante no es 0, así que la matriz es invertible.
Por tanto, sustituyendo el valor del determinante en la fórmula, la inversa de la matriz será:
Ahora tenemos que calcular la matriz adjunta de A. Para ello, debemos sustituir cada elemento de la matriz A por su adjunto.
Recuerda que para calcular el adjunto de , es decir, del elemento de la fila
y de la columna
, hay que aplicar la siguiente fórmula:
Donde el menor complementario de es el determinante de la matriz eliminando la fila
y la columna
.
Por tanto, los adjuntos de los elementos de la matriz A son:
Comentario: No confundas el determinante 1×1 con el valor absoluto, ya que en el determinante 1×1 no se convierte el número en positivo.
Una vez hemos calculado los adjuntos, tan solo tenemos que sustituir los elementos de A por sus adjuntos para hallar la matriz adjunta de A:
Comentario: en algunos sitios la matriz adjunta es la traspuesta de la matriz adjunta que hemos definido aquí.
Por tanto, sustituimos la matriz adjunta en la fórmula de la matriz inversa y queda:
El exponente nos indica que tenemos que trasponer la matriz. Y para trasponer una matriz hay que cambiar sus filas por columnas, es decir, la primera fila de la matriz pasa a ser la primera columna de la matriz, y la segunda fila pasa a ser la segunda columna:
Y, por último, multiplicamos cada término de la matriz por
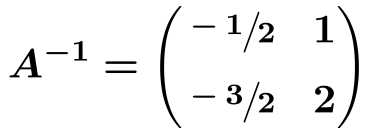
Ejercicios resueltos de matrices inversas con el método de los determinantes (o de la matriz adjunta)
Ejercicio 1
Invierte la siguiente matriz de dimensión 2×2 por el método de la matriz adjunta:
La fórmula de la matriz inversa es:
Primero calculamos el determinante de la matriz:
El determinante es diferente de 0, por lo tanto, sí que se puede invertir la matriz.
Ahora calculamos la matriz adjunta de A:
Una vez calculados el determinante de la matriz y su adjunta, sustituimos sus valores en la fórmula:
Trasponemos la matriz adjunta:
De manera que la matriz inversa de A es:
Ejercicio 2
Invierte la siguiente matriz cuadrada por el método de los determinantes:
La fórmula de la matriz inversa es:
Primero calculamos el determinante de la matriz:
El determinante es diferente de 0, por lo tanto, sí que se puede invertir la matriz.
Ahora calculamos la matriz adjunta de A:
Una vez hallados el determinante de la matriz y su adjunta, sustituimos sus valores en la fórmula:
Transponemos la matriz adjunta:
Multiplicamos cada elemento por
Así que la matriz inversa de A es:
Ejercicio 3
Invierte la siguiente matriz de dimensión 3×3 por el método de la matriz adjunta:
La fórmula de la matriz inversa es:
En primer lugar resolvemos el determinante de la matriz con la regla de Sarrus:
El determinante es diferente de 0, por lo tanto, sí que se puede invertir la matriz.
Una vez hemos resuelto el determinante, hallamos la matriz adjunta de A:
Una vez hemos calculado el determinante de la matriz y su adjunta, sustituimos sus valores en la fórmula:
Trasponemos la matriz adjunta:
Y la matriz A invertida es:
Ejercicio 4
Invierte la siguiente matriz de orden 3 por el método de la matriz adjunta:
La fórmula de la matriz inversa es:
Primero tenemos que calcular el determinante de la matriz, ya que si el determinante es 0 significa que la matriz no tiene inversa.
El determinante de A es 0, por lo que la matriz no se puede invertir.
Ejercicio 5
Invierte la siguiente matriz cuadrada 3×3 por el método de la matriz de los determinantes:
La fórmula de la matriz inversa es:
Primero de todo resolvemos el determinante de la matriz con la regla de Sarrus:
El determinante es distinto de 0, por lo tanto, sí que se puede invertir la matriz.
Una vez hemos resuelto el determinante, hallamos la matriz adjunta de A:
Una vez hemos calculado el determinante de la matriz y su adjunta, sustituimos sus valores en la fórmula:
Trasponemos la matriz adjunta:
Y, por último, operamos:
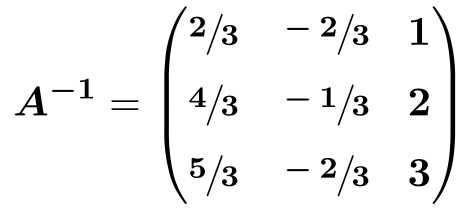
Invertir una matriz por el método de Gauss:
Para calcular la inversa de una matriz con el método de Gauss, se tienen que hacer operaciones en las filas de una matriz (lo veremos más abajo). Así que antes de ver cómo utilizar método de Gauss, es importante que sepas todas las operaciones que se pueden hacer en las filas de las matrices:
Transformaciones de filas permitidas en el método de Gauss
- Cambiar el orden de las filas de la matriz.
Por ejemplo, podemos cambiar de orden las filas 2 y 3 de una matriz:
- Multiplicar o dividir todos los términos de una fila por un número diferente de 0.
Por ejemplo, podemos multiplicar la fila 1 por 4, y dividir la fila 3 entre 2:
- Sustituir una fila por la suma de la misma fila más otra fila multiplicada por un número.
Por ejemplo, en la siguiente matriz sumamos a la fila 2 la fila 3 multiplicada por 1:
Ejemplo de cómo calcular la matriz inversa por el método Gauss:
Vamos a ver con un ejemplo cómo aplicar el método de Gauss para invertir una matriz:
- Calcula la inversa de la siguiente matriz:
Lo primero que debemos hacer es poner la matriz A y la matriz Identidad en una sola matriz. La matriz A en la parte izquierda y la matriz Identidad en la parte derecha:
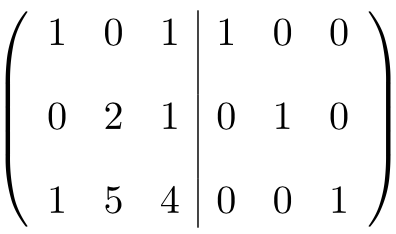
Para calcular la matriz inversa, tenemos que convertir la matriz de la parte izquierda en la matriz identidad. Y, para ello, debemos aplicar transformaciones en las filas hasta conseguirlo.
Iremos por columnas, es decir, haremos operaciones en las filas para transformar primero los números de la primera columna, luego los de la segunda columna, y finalmente los de la tercera columna.
El 1 y el 0 de la primera columna ya están bien, ya que la matriz identidad también tiene un 1 y un 0 en esas posiciones. Por tanto, no hace falta aplicar ninguna transformación en estas filas de momento.
Sin embargo, la matriz identidad tiene un 0 en el último elemento de la primera columna, donde ahora tenemos un 1. Por tanto, tenemos que convertir el 1 en un 0. Para ello, sumamos a la fila 3 la fila 1 multiplicada por -1:
De manera que si hacemos esta suma nos queda la siguiente matriz:
De esta forma hemos conseguido transformar el 1 en un 0.
Pasamos ahora a la segunda columna de la matriz de la izquierda. El primer elemento es un 0, que ya está bien porque la matriz identidad tiene un 0 en esa misma posición. Sin embargo, en vez de un 2 debería haber un 1, por tanto, dividimos la segunda fila entre 2:
Además, de la segunda columna también tenemos que transformar el 5 en un 0. Pues como el 5 es cinco veces más grande que el 1 de la segunda fila, sumaremos a la fila 3 la fila 2 multiplicada por -5:
Por tanto, al hacer esta operación nos queda la matriz con un 0 en el último elemento de la segunda columna:
Finalmente, vamos a transformar la última columna de la matriz de la izquierda, pero esta vez debemos empezar desde abajo. Así que tenemos que transformar el en un 1. Por tanto, multiplicamos la última fila por 2:
Ahora tenemos que transformar el restante de la última columna en un 0. Sin embargo, esta vez no podemos multiplicar la fila por 2, ya que también convertiríamos el 1 en un 2 (cuando la matriz identidad tiene un 1 en esa posición). Por tanto, sumaremos a la fila 2 la fila 3 dividida entre -2:
De manera que al hacer esta operación conseguimos transformar el en un 0:
Por último, solo nos falta transformar en un 0 el 1 de la primera fila de la tercera columna. La tercera fila también tiene un 1 en esa misma columna, por tanto, sumaremos a la fila 1 la fila 3 multiplicada por -1:
Y al hacer esta operación conseguimos convertir el 1 en un 0:
Una vez hemos conseguido convertir la matriz de la izquierda en la matriz identidad, también sabemos la matriz inversa. Porque la matriz inversa es la matriz que obtenemos en la parte derecha al convertir la matriz de la izquierda en la matriz identidad. De modo que la inversa de la matriz es:
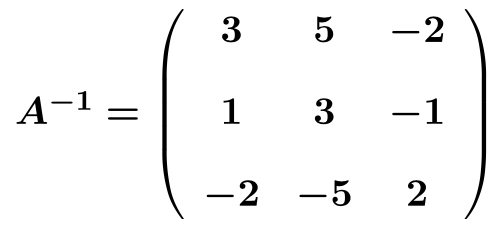
Ejercicios resueltos de matrices inversas con el método de Gauss
Ejercicio 1
Invierte la siguiente matriz a través del método de Gauss:
Lo primero que debemos hacer es poner la matriz A y la matriz Identidad en una sola matriz. La matriz A en la parte izquierda y la matriz identidad en la parte derecha:
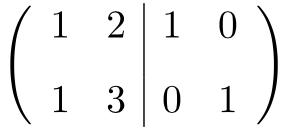
Ahora, para calcular la matriz inversa, tenemos que convertir la matriz de la parte izquierda en la matriz identidad. Y, para ello, debemos aplicar transformaciones en las filas hasta conseguirlo.
El primer término de todos, el 1, ya es igual que la matriz identidad. Por tanto, no hace falta aplicar ninguna transformación en la primera fila de momento.
Sin embargo, la matriz identidad tiene un 0 en el último elemento de la primera columna, donde ahora tenemos un 1. Así que tenemos que convertir el 1 en un 0. Para ello, a la fila 2 le restamos la fila 1:
Pasamos a la segunda columna: el 1 de abajo ya está bien. Pero el 2 de arriba no, ya que la matriz identidad tiene un 0 en esa posición. Por tanto, para convertir el 2 en un 0, a la fila 1 le restamos la fila 2 multiplicada por 2:
La matriz inversa es la matriz que obtenemos en la parte derecha tras convertir la matriz de la izquierda en la matriz identidad. Y ahora ya hemos conseguido la matriz identidad en la parte izquierda. Por tanto, la matriz inversa es:
Ejercicio 2
Invierte la siguiente matriz con el procedimiento de Gauss:
En primer lugar, ponemos la matriz A y la matriz Identidad en una sola matriz:
Ahora tenemos que ir transformando las filas hasta convertir la matriz de la parte izquierda en la matriz identidad.
La primera columna de la matriz de la izquierda ya es igual que la primera columna de la matriz identidad. Por tanto, no hace falta cambiar ninguno de sus números.
Sin embargo, la matriz identidad tiene un 1 en el segundo elemento de la segunda columna, donde ahora hay un 3. Así que tenemos que convertir el 3 en un 1. Para ello, a la fila 2 le restamos la fila 3 multiplicada por 2:
La matriz identidad tiene un 0 en el último elemento de la segunda columna, donde ahora hay un 1. Así que tenemos que convertir el 1 en un 0. Para ello, a la fila 3 le restamos la fila 2:
La matriz identidad tiene un 0 en el primer elemento de la segunda columna, donde ahora hay un 1. Así que tenemos que convertir el 1 en un 0. Para ello, a la fila 1 le restamos la fila 2:
Ahora solo nos falta convertir el -4 en 0. Para ello, a la fila 1 le sumamos la fila 3 multiplicada por 4:
Ya hemos conseguido la matriz identidad en la parte izquierda. Por tanto, la matriz inversa es:
Ejercicio 3
Invierte la siguiente matriz por el método de Gauss:
Antes de empezar a operar tenemos que poner la matriz A y la matriz Identidad en una sola matriz:
Ahora debemos convertir la matriz de la parte izquierda en la matriz identidad operando en las filas.
Los dos primeros elementos de la primera columna ya son iguales que los de la matriz identidad. Por tanto, no hace falta cambiar ninguno de estos números.
Pero la matriz identidad tiene un 0 en el tercer elemento de la primera columna, donde ahora hay un 2. Así que tenemos que convertir el 2 en un 0. Para ello, a la fila 3 le restamos la fila 1 multiplicada por 2:
La matriz identidad tiene un 0 en el primer elemento de la segunda columna, donde ahora hay un 2. Así que tenemos que convertir el 2 en un 0. Para ello, a la fila 1 le restamos la fila 2 multiplicada por 2:
La matriz identidad tiene un 0 en el último elemento de la segunda columna, donde ahora hay un -4. Así que tenemos que convertir el -4 en un 0. Para ello, a la fila 3 le sumamos la fila 2 multiplicada por 4:
Ahora solo nos falta convertir el primer elemento de la tercera columna en 0. Para ello, a la fila 1 le sumamos la fila 3 multiplicada por -1:
Ya hemos logrado que la matriz de la izquierda sea la matriz identidad. De manera que la inversa de la matriz es:
Ejercicio 4
Invierte la siguiente matriz por el método de Gauss:
Lo primero que debemos hacer es juntar la matriz A y la matriz Identidad en una sola matriz:
Ahora debemos convertir la matriz de la parte izquierda en la matriz identidad aplicando operaciones en las filas.
El primer elemento de la primera columna ya es igual que el de la matriz identidad. Por tanto, no hace falta cambiarlo.
Sin embargo, la matriz identidad tiene un 0 en el segundo elemento de la primera columna, donde ahora hay un 1. Así que tenemos que convertir el 1 en un 0. Para ello, a la fila 2 le restamos la fila 1:
Pasamos a la segunda columna: primero transformamos el 4 en un 1 dividiendo la segunda fila entre 4:
La matriz identidad tiene un 0 en el primer elemento de la segunda columna, donde ahora hay un -2. Así que tenemos que convertir el -2 en un 0. Para ello, a la fila 1 le sumamos la fila 2 multiplicada por 2:
La matriz identidad tiene un 0 en el último elemento de la segunda columna, donde ahora hay un 3. Así que tenemos que convertir el 3 en un 0. Para ello, a la fila 3 le restamos la fila 2 multiplicada por 3:
Pasamos a la tercera columna: debemos transformar el último en un 1. Para ello, multiplicamos la tercera fila por 2:
La matriz identidad tiene un 0 en el segundo elemento de la última columna. Así que tenemos que convertir el en un 0. Para ello, a la fila 2 le restamos la fila 3 dividida entre 2:
Ahora tan solo nos falta convertir el primer elemento de la tercera columna en 0. Para ello, a la fila 1 le restamos la fila 3:
Por lo tanto, la matriz inversa es:
Por último, se pueden simplificar las fracciones de la matriz inversa:
Propiedades de la matriz inversa
La matriz inversa tiene las siguientes características:
- La inversa de una matriz es única.
- La inversa de la matriz inversa es la matriz original:
- La inversa de la multiplicación de dos matrices es igual al producto de las inversas de las matrices pero cambiando su orden.
- Trasponer una matriz y después hacer la inversa de la matriz es lo mismo que hacer primero la inversión de la matriz y luego trasponerla.
- Para resolver el determinante de la inversa de una matriz podemos calcular el determinante de la matriz y luego hacer su inverso, ya que ambas operaciones dan el mismo resultado.
Fórmula para calcular rápidamente la inversa de una matriz 2×2
Como hemos visto, cualquier matriz se puede invertir por el método de los determinantes o por el método de Gauss. Pero, a parte, también existe una fórmula para hallar la inversa de una matriz 2×2 de una manera muy rápida:
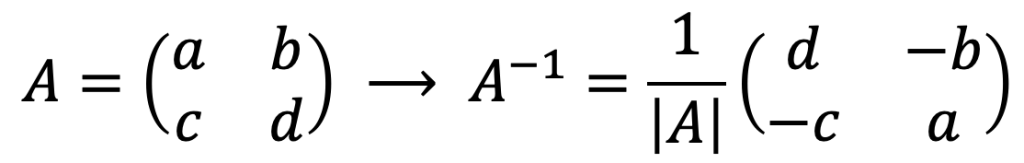
Como ves, invertir una matriz de dimensión 2×2 es sencillo: solo hace falta resolver el determinante de la matriz , alternar de posición los elementos de la diagonal principal, y cambiar de signo los elementos de la diagonal secundaria.
Ejemplo de cómo sacar una matriz inversa 2×2 con la fórmula
Calcula la inversa de la siguiente matriz cuadrada 2×2:
El determinante de la matriz A es:
Ahora aplicamos la fórmula de la matriz inversa:
Y multiplicamos la matriz por la fracción:
De forma que la matriz A invertida es:
Como puedes ver, invertir una matriz con esta fórmula es mucho más rápido, pero solo se puede utilizar en matrices de dimensión 2×2.
Ejercicios resueltos de matrices inversas 2×2 con la fórmula
Ejercicio 1
Invierte la siguiente matriz de dimensión 2×2:
El determinante de la matriz A es:
Ahora aplicamos la fórmula para hallar la matriz inversa:
Por lo tanto, la inversa de la matriz A es:
Ejercicio 2
Calcula la inversa de la siguiente matriz de orden 2:
El determinante de la matriz A es:
Ahora aplicamos la fórmula para resolver la matriz inversa de dimensión 2×2:
Y, por último, hacemos la multiplicación:
Ejercicio 3
Invierte la siguiente matriz 2×2:
El determinante de la matriz A es:
Ahora aplicamos la fórmula para calcular la matriz inversa de dimensión 2×2:
Y, finalmente, hacemos el producto entre la fracción y la matriz:
Ejercicio 4
Halla la inversa de la siguiente matriz de segundo orden:
El determinante de la matriz A es:
Ahora aplicamos la fórmula para hacer la matriz inversa de dimensión 2×2:
Y, por último, hacemos la multiplicación:
Resolver un sistema de ecuaciones con la matriz inversa
Es difícil poder apreciar las aplicaciones reales de la inversa de una matriz. De hecho, seguro que te estás preguntando… ¿para qué sirve la matriz inversa? ¿realmente se usa para algo?
Pues una de las utilidades de la matriz inversa es la resolución de sistemas de ecuaciones lineales. Y sí, aunque pueden sonar dos conceptos muy diferentes, sí que es posible hallar la solución de un sistema de ecuaciones invirtiendo una matriz.
Veamos con un ejemplo cómo se hace:
- Calcula la solución del siguiente sistema de ecuaciones con la matriz inversa:
Primero de todo, debemos observar que un sistema de ecuaciones se puede expresar en forma de matrices:
Se puede comprobar que esta forma matricial del sistema es equivalente a la expresión con ecuaciones: si hacemos la multiplicación de las matrices veremos que obtenemos las dos ecuaciones del sistema.
Ahora, para simplificar los siguientes pasos, llamaremos a la matriz que tiene los coeficientes de las incógnitas,
a la matriz columna con las incógnitas, y
a la matriz columna con los términos independientes:
De manera que la matriz es la incógnita de la ecuación matricial.
Para solucionar esta ecuación matricial, se debe seguir todo un procedimiento que aquí no explicaremos tan detalladamente. Si quieres entenderlo completamente puedes repasar cómo resolver ecuaciones con matrices, donde explicamos paso a paso todo el proceso.
Este procedimiento se basa en una propiedad de las matrices inversas: cualquier matriz multiplicada por su inversa es igual a la matriz Identidad (o Unidad). Por tanto, se puede despejar fácilmente la matriz incógnita multiplicando ambos miembros de la ecuación por la inversa de la matriz A:
Y una vez hemos aislado la matriz , calculamos la inversa de
y resolvemos el producto de matrices:
Por lo tanto, la solución del sistema de ecuaciones es:

En el ejemplo inicial para describir el método Gauss hay un pequeño error en la descripción:
«Ejemplo de cómo calcular la matriz inversa por el método Gauss:
….Finalmente, vamos a transformar la última columna de la matriz de la izquierda […] tenemos que transformar el 1/2 en un 2. Por tanto…»
Creo que debería decir: «tenemos que transformar el 1/2 en 1. Por tanto…»
La página es muy buena, bien explicados los conceptos, bien descritos los ejemplos y bien diseñada la página para facilitar navegar. Les felicito!
Tienes toda la razón Augusto. Evidentemente se debe transformar el 1/2 en 1, ya que la matriz Identidad tiene un 1 en esa posición. Lo acabamos de rectificar.
De hecho, aunque en la explicación ponía un 2, en la operación se estaba transformando por un 1 correctamente. 🤦♂️
Muchas gracias por tu comentario, siempre recibimos con gusto cualquier felicitación y cualquier aportación que nos permita mejorar. 👌
MI NOMBRE ES MGUEL HERNANDEZ
ME PODRIAN DECIR SI HAY AGUNA MANERA DE TRANSFORMAR UNA MATRIZ SINGULAR A NO SINGULAR, SI LA HAY ME PODRIAN DECIR DONDE INVESTIGAR
SALUDOS
Hola Miguel,
En primer lugar, he eliminado el e-mail de tu comentario para evitar que te envíen mensajes de spam. Créeme, son muchos.😂
Contestando a tu pregunta, la respuesta es no. No existe ningún método para transformar una matriz singular a una matriz no singular (matriz regular).
Principalmente, se distingue entre una matriz singular y una regular por su determinante: si el determinante es nulo se trata de una matriz singular, pero si el determinante es distinto de cero la matriz es regular. Sin embargo, el resultado del determinante de una matriz no puede pasar de ser nulo a dar cualquier otro valor independientemente de las operaciones que le apliques a la matriz (puedes buscar la explicación de las propiedades de los determinantes en esta web). La única manera de lograr eso sería cambiando un número de la matriz, pero entonces ya es otra matriz distinta.
Al final, una matriz es la representación matemática de un sistema y, por tanto, las características de una matriz van ligadas al tipo de sistema. Entonces, para que una matriz sea de diferente tipo tendría que cambiar el propio sistema.
Espero haberme explicado, ¡cualquier duda me dices!
¡Saludos!