Cómo calcular el determinante de una matriz 2×2

En esta página aprenderás qué es el determinante de una matriz 2×2. Además, encontrarás ejemplos y ejercicios resueltos paso a paso sobre cómo resolver determinantes de orden 2, para que puedes practicar y entenderlo a la perfección.

Sumario
1. ¿Qué es un determinante 2×2?
2. ¿Cómo resolver un determinante de orden 2?
3. Ejemplos de cómo calcular determinantes 2×2:
4. Ejercicios resueltos de determinantes de matrices 2×2

¿Qué es un determinante 2×2?

Un determinante de orden 2 es una matriz de dimensión 2×2 representada con una barra vertical a cada lado de la matriz. Por ejemplo, si tenemos la siguiente matriz:

\displaystyle A = \begin{pmatrix} 3 & 1 \\[1.1ex] 5 & 2 \end{pmatrix}

El determinante de la matriz A se representa de la siguiente forma:

\displaystyle \lvert A \rvert = \begin{vmatrix} 3 & 1 \\[1.1ex] 5 & 2 \end{vmatrix}

Como has visto, escribir el determinante de una matriz cuadrada 2×2 es sencillo. Ahora vamos a ver cómo se calcula:

¿Cómo resolver un determinante de orden 2?

Para calcular el determinante de una matriz 2×2 tenemos que multiplicar los elementos de la diagonal principal y restarle el producto de la diagonal secundaria.

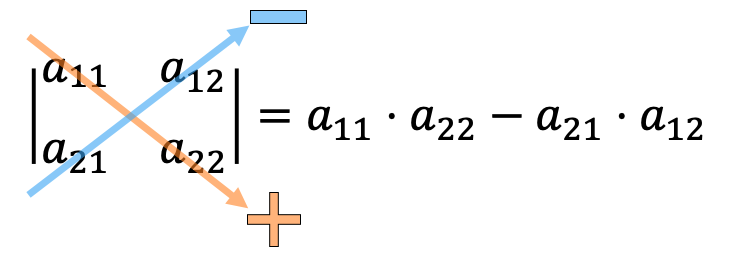
ejemplo de como calcular el determinante de una matriz 2x2

Ejemplos de cómo calcular determinantes 2×2:

\displaystyle\begin{vmatrix} 3 & 4 \\[1.1ex] 2 & 1 \end{vmatrix} = 3 \cdot 1 - 2 \cdot 4 = 3 - 8 = \bm{-5}

\displaystyle\begin{vmatrix} 2 & -3 \\[1.1ex] 1 & 5 \end{vmatrix} = 2 \cdot 5 - 1 \cdot (-3) =10-(-3) = 10+3= \bm{13}

 

Ejercicios resueltos de determinantes de matrices 2×2

Ejercicio 1

Calcula el siguiente determinante 2×2:

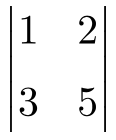
ejercicio resuelto paso a paso de determinante 2x2

Para hacer un determinante 2×2 tenemos que multiplicar los elementos de la diagonal principal y restarle el producto de la diagonal secundaria:

\displaystyle \begin{vmatrix} 1 & 2 \\[1.1ex] 3 & 5 \end{vmatrix} = 1 \cdot 5 - 3 \cdot 2 = 5 - 6 = \bm{-1}

 

Ejercicio 2

Resuelve el siguiente determinante de dimensión 2×2:

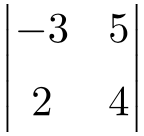
ejercicios resueltos paso a pas de determinantes 2x2

Para hallar la solución de un determinante de orden 2 debemos multiplicar los elementos de la diagonal principal y restarle el producto de la diagonal secundaria:

\displaystyle \begin{vmatrix} -3 & 5 \\[1.1ex] 2 & 4 \end{vmatrix} = -3 \cdot 4 - 2 \cdot 5 = -12 - 10 = \bm{-22}

 

Ejercicio 3

Halla la solución del siguiente determinante de orden 2:

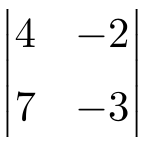
ejercicio resuelto paso a paso de un determinante de una matriz 2x2

Para encontrar la solución de un determinante de dimensión 2 hay que multiplicar los elementos de la diagonal principal y restarle el producto de la diagonal secundaria:

\displaystyle \begin{vmatrix} 4 & -2 \\[1.1ex] 7 & -3\end{vmatrix} = 4 \cdot (-3) - 7 \cdot (-2) = -12 - (-14) =-12+14= \bm{2}

 

Ejercicio 4

Calcula el siguiente determinante 2×2:

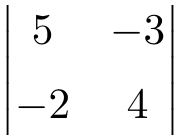
como resolver el determinante de una matriz 2x2 , ejercicio resuelto paso a paso

Para calcular determinantes de matrices 2×2 tenemos que multiplicar los elementos de la diagonal principal y restarle el producto de la diagonal secundaria:

\displaystyle \begin{vmatrix} 5 & -3 \\[1.1ex] -2 & 4\end{vmatrix} = 5 \cdot 4 - (-2) \cdot (-3) = 20 - (+6) = \bm{14}

 

Ejercicio 5

Determina el resultado del siguiente determinante 2×2:

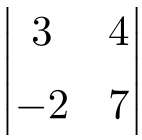
ejercicio resuelto de como resolver el determinante de una matriz de orden 2 paso a paso

Para hallar la solución a un determinante 2×2 tenemos que multiplicar los elementos de la diagonal principal y restarle el producto de la diagonal secundaria:

\displaystyle \begin{vmatrix} 3 & 4 \\[1.1ex] -2 & 7\end{vmatrix} = 3 \cdot 7 - (-2) \cdot 4 = 21 - (-8)=21+8 = \bm{29}

 

¡Genial! ¡Ya sabes hacer determinantes de dimensión 2×2! Ahora seguro que ya eres capaz de entender cómo se calcula el determinante 3×3 y también cómo se resuelve el determinante de una matriz 4×4.

10 comentarios en “Cómo calcular el determinante de una matriz 2×2”

    1. Matrices y Determinantes

      Hola Jackelin,

      Se trata de una matriz 2×2, por lo que debes multiplicar en cruz y luego restar los productos para obtener el resultado del determinante 2×2:

      \displaystyle\begin{vmatrix}-8&2\\[1.1ex]-3&2\end{vmatrix}=-8\cdot 2- (-3)\cdot 2=-16-(-6)=-10

      Responder

Deja un comentario

Tu dirección de correo electrónico no será publicada. Los campos obligatorios están marcados con *

Ir arriba